[ad_1]
The 1982 SAT infamously held a math dilemma so challenging that even its creators didn’t include a correct reply. The botch necessary the rescoring of 300,000 tests, scholastic victims of the knotty coin rotation paradox.
Here’s how the paradox will work: Location two quarters flat on a table so that they are touching. Keeping a person coin stationary on the desk, roll the other quarter all around it, keeping edge contact amongst the two devoid of slipping. When the transferring quarter returns to its beginning place, how lots of entire rotations has it manufactured? In other terms, how quite a few periods has George Washington returned to his upright place in the graphic below? If you dig puzzles like this, acquire a minute to feel about it.
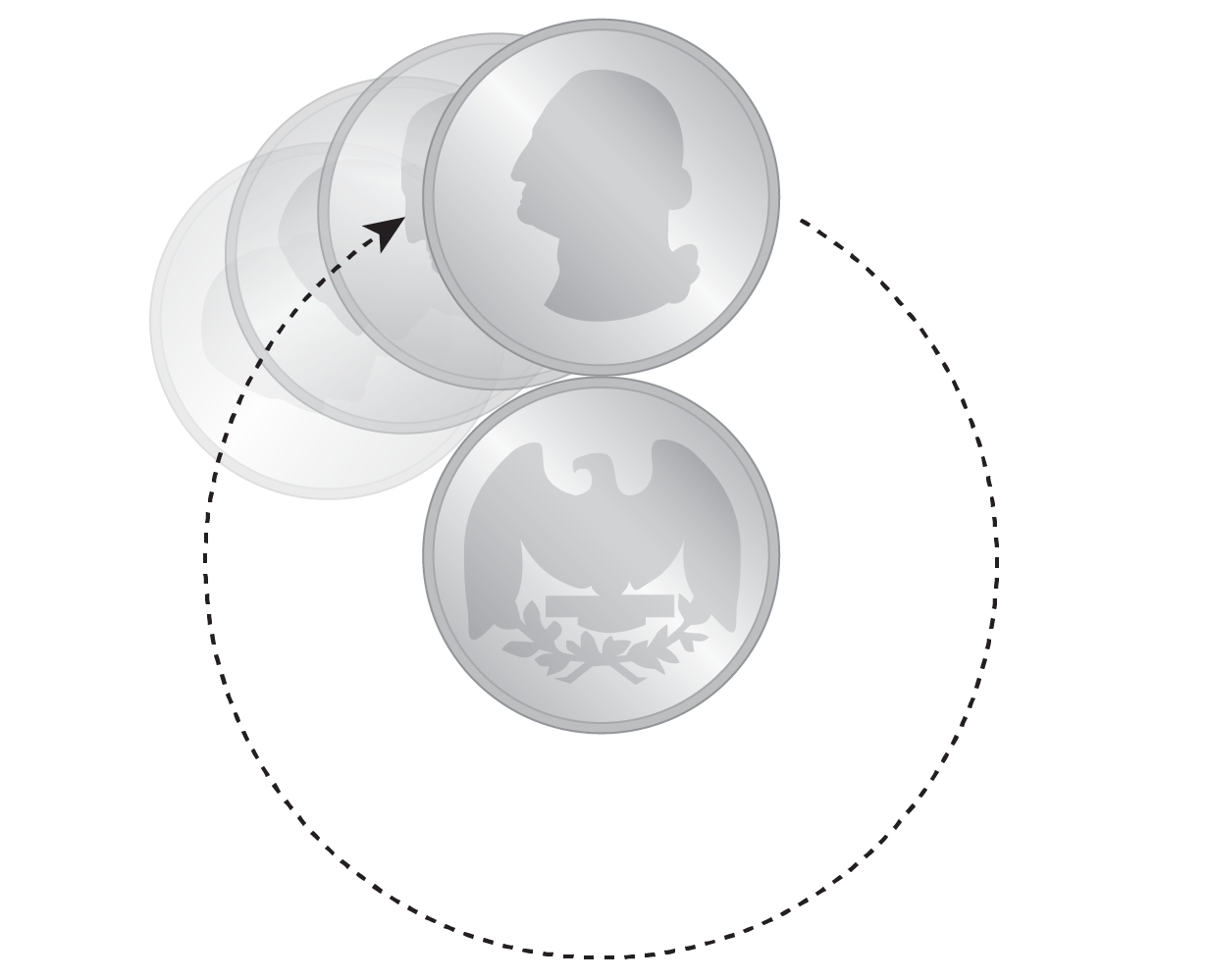


Lots of men and women suspect that George will make a single entire rotation. A quarter’s circumference is about three inches all over. So the going quarter rolls along a route with a duration of a few inches, the same distance as its personal circumference. If we wrap a string all-around a quarter and roll it along a a few-inch path, unfurling the string as we go, then surely 3 inches of string will unfurl—just plenty of for a one rotation.
In simple fact, the relocating quarter would make precisely two comprehensive rotations by the time it returns to its authentic posture. The phenomenon defies prevalent sense. If you obtain it hard to acknowledge, I inspire you to take a look at it for yourself. Any two disks of equivalent measurement will do.
Linked: Why the ‘Sleeping Splendor Problem’ Is Retaining Mathematicians Awake
The edition of this challenge that snuck its way onto the 1982 SAT math area experienced a compact variation: the centre disk was greater than the 1 rolling all-around it. Here’s a variation of that issue, with the wording marginally modified for clarity:
The radius of circle B is three situations the radius of circle A. Setting up from the placement revealed in the determine, circle A rolls about circle B. When circle A returns to its starting off place, how numerous rotations will it have done?
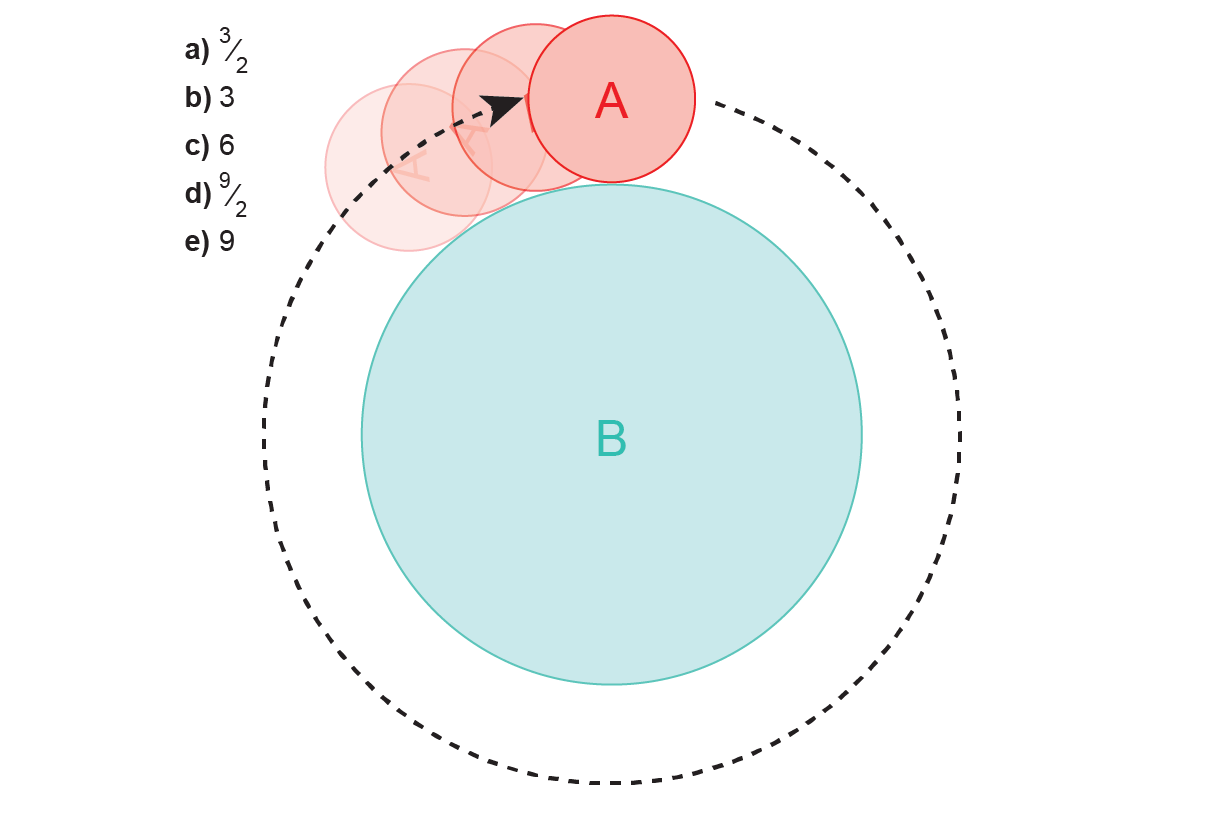


Does that appear to be acquainted? Listed here, we’re explained to the larger circle’s radius is a few times that of the scaled-down circle. This implies the identical for the circumferences of the two circles: B is 3 times for a longer time all-around its perimeter than A. It is tempting to purpose that the smaller circle could “unwrap” itself specifically a few occasions to encase the bigger one particular. So “3” was the meant several-alternative answer on the SAT. In reality, circle A tends to make four rotations on its trip—again, particularly one far more rotation than instinct expects. The paradox was so much from the check writers’ awareness that 4 was not provided as an option among the probable answers, so even the most astute learners ended up forced to submit a incorrect reaction. Three of the 300,000 learners who took the exam that contains the query claimed the problem to the College Board, and each individual examination had to be rescored.
So why is there an extra rotation? The strategy that led us astray earlier mentioned does contain some knowledge. Rolling a quarter along a 3-inch straight-line path would include only just one rotation. Also, a compact circle rolling in a straight line with a length that is three moments its diameter would rotate a few moments. So the circular form of the path in some way leads to a rotation of its individual. To see why, picture rolling a quarter around the perimeter of a small poppy seed. George will rotate once even while the duration all around the seed is negligible. So there are two sources of rotation: one particular from rolling alongside a route (the for a longer period it is, the far more rotations) and an additional from revolving about an object, which contributes a person rotation regardless of its sizing.
Yet another beneficial perspective will come from imagining rolling a quarter all around a sq.. Each edge of the square is a straight-line section, and George’s head will spin at the time for every a few inches of duration, but the second you arrive at a corner, the quarter will have to rotate farther to crystal clear that corner. (Once again, attempt this for yourself if it’s tricky to photograph.) It turns out that this excess rotation at the corners is just 90 degrees, which final results in 1 entire rotation (360 levels) by the time the coin traverses all 4 corners of the square and returns to its get started. Similarly, rolling all over a triangle would entail 120-diploma rotations around every corner.
The outcome scales up to celestial bodies. The moon famously has a dim facet and generally exhibits the similar confront to us Earthlings. Quite a few people today erroneously interpret the unchanging view of the moon to imply that it should not spin about its axis like Earth does. If the moon didn’t spin during its orbit, although, we would see its darkish aspect from some destinations on Earth. You can show this with your have fists—hold a person continual and orbit the other all over it, devoid of any rotation. Observers standing on a person of your stationary knuckles will get a diverse glimpse of the orbiting fist at distinct moments. To eternally cover its derriere, the moon has to rotate after each and every time it completes an orbit. (This best parity in between orbit time and rotation time is not an astronomical coincidence but instead an case in point of a phenomenon called tidal locking. We’re also sidelining our relativistic reference body, with apologies to Albert Einstein.) With the cash and the SAT challenge, we saw that there were being two sources of rotation: some from “straight-line” rolling alongside any path and a single excess from revolving around an item. The moon doesn’t do any straight-line rolling. If the Earth were being flat, the moon would glide higher than it without having rolling. So the single rotation of the moon is completely due to the fact of its revolution about the very spherical Earth.
If you had an aerial see of the photo voltaic procedure, how quite a few instances would you see Earth entire a rotation in a regular calendar year? Several would say 365, but nevertheless once more, they would slide a person limited of the correct reply: 366. (Take note this has nothing to do with leap many years, which are a absolutely separate issue.) Humanity has outlined a day to be the quantity of time it can take for the sunshine to return to the same place in the sky. It is easy to usually have the sun straight overhead at noon. But when Earth completes one rotation, the sunlight basically has not very returned to its perch in the sky yet. Let us revisit the SAT diagram to see what’s likely on—only this time we’ll mark a set dot on the modest circle and notice what happens to the dot as that circle rolls all around the massive one particular:
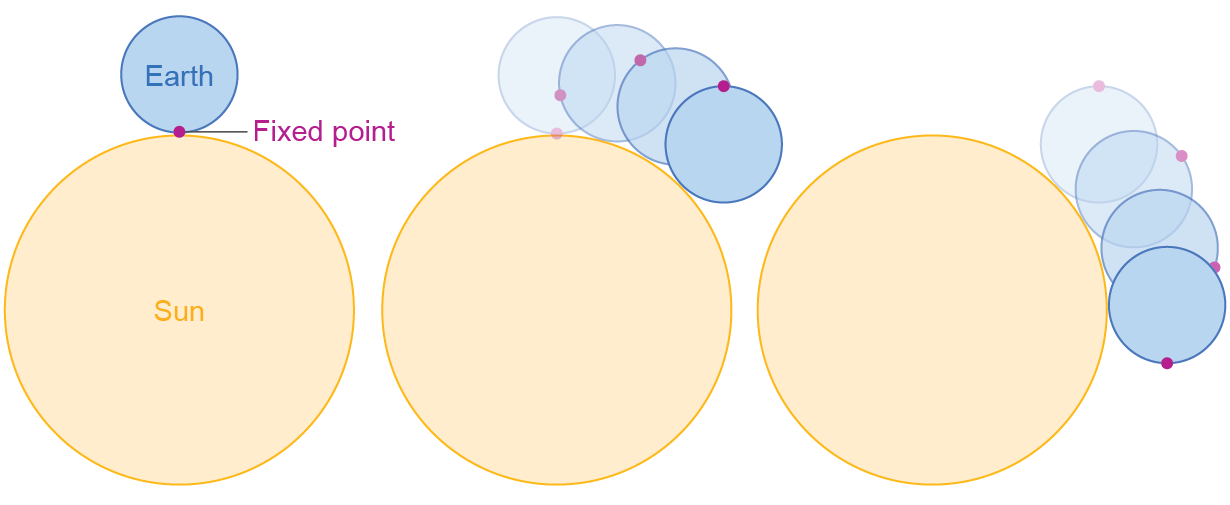


Imagine of the significant circle as the solar, the very little circle as Earth (not to scale) and the dot as a set position on our world. In the initially panel, the dot stares specifically at the sun. It is exactly noon. In the final panel, the little circle has finished a entire rotation (the dot details down once more), but see that it is not midday for another person standing at the dot. The modest circle would require to edge forward a minor over and above a person rotation for the dot to kiss the big circle all over again. Also, although Earth completes a rotation in 23 hours and 56 minutes (which is termed a sidereal working day), it will take 4 extra minutes for the sun to return to its overhead place in the sky, yielding our definition of a 24-hour day. Over the study course of 365 days, these 4 further minutes of rotation for every working day incorporate up to 1 additional rotation.
Thanks for rolling together with us on this tour of coins, testing problems and planetary motion—it’s adequate to make anyone’s head spin.
[ad_2]
Supply link






