Open your beloved social media platform and note how quite a few pals or followers you have. Especially, observe the very first digit of this amount. For example, if you have 400 close friends, the foremost digit is 4, and if you have 79, it is 7. Let’s say we asked many individuals to do this. We could possibly count on responses throughout the board, as prevalent intuition implies that pal counts should really be to some degree random and as a result their foremost digits really should be way too, dealing with 1 via 9 similarly. Surprisingly, this is not what we would uncover. Rather, we would see a steep imbalance wherever virtually 50 percent of persons have mate counts commencing with 1 or 2, while a paltry 10 percent start with 8 or 9. Try to remember, this is not about having additional or fewer friends: owning 1,000 buddies is way extra than acquiring 8.

This strange overrepresentation of 1s and 2s extends beyond close friends and followers to likes and retweets, and very well further than social media to many corners of the numerical globe: place populations, river lengths, mountain heights, loss of life costs, stock selling prices, even the assorted assortment of quantities uncovered in a standard difficulty of Scientific American. Not only are smaller foremost digits a lot more prevalent, but they comply with a specific and regular pattern.

If all digits were being represented equally, as one particular would naively assume, then they would every show up a person ninth (about 11.1 per cent) of the time. Nonetheless, in an uncanny variety of authentic-earth data sets, an astonishing 30.1 per cent of the entries start with a 1, 17.6 percent begin with a 2, and so on. This phenomenon is recognized as Benford’s legislation. The legislation even persists when you improve the units of your data. Measure rivers in feet or furlongs, measure inventory charges in bucks or dinars, any way you measure, these exact proportions of major digits persevere. Whilst mathematicians have proposed quite a few intelligent motives for why the sample could emerge, its sheer ubiquity evades a straightforward explanation. 

It may appear like a mild observation, but Benford’s legislation has been utilised to effective influence to set individuals powering bars and detect huge functions of fraud.

&#13

&#13
&#13

&#13

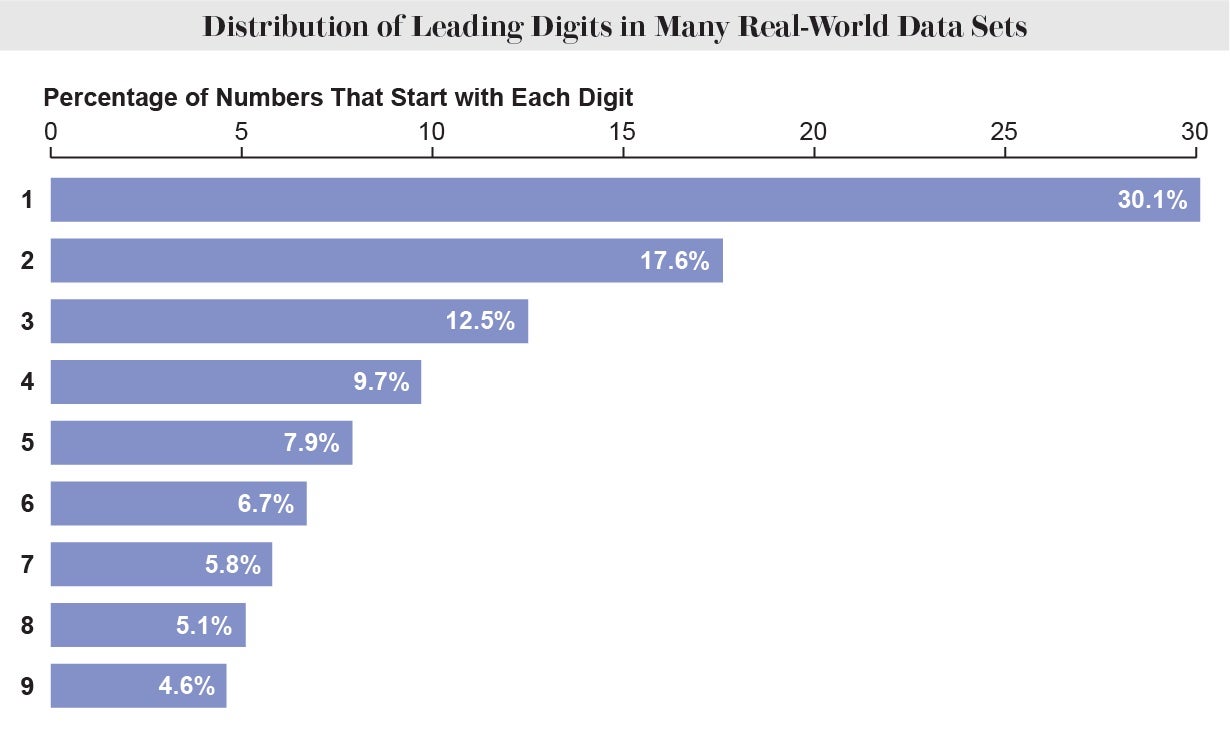
Prior to calculators, individuals outsourced hairy arithmetic to reference books termed logarithm tables. In 1881, astronomer Simon Newcomb observed that early webpages of logarithm tables, which correspond to quantities beginning with just one, ended up grubby and worn as opposed with the pristine later on internet pages. He deduced that smaller sized leading digits need to be a lot more popular in all-natural info sets, and he published the proper percentages. Physicist Frank Benford built the same observation in 1938 and popularized the regulation, compiling additional than 20,000 information details to display its universality. Digression: Benford’s eponymous credit rating is an instance of Stigler’s legislation, which contends that scientific discoveries are under no circumstances named after their first discoverer. Stigler’s law was asserted by sociologist Robert K. Merton perfectly ahead of Stephen Stigler obtained his identify on it. 

Benford’s regulation is not just a statistical oddity: financial advisor Wesley Rhodes was convicted of defrauding investors when prosecutors argued in court docket that his paperwork did not accord with the anticipated distribution of foremost digits, and they had been as a result very likely fabricated. The basic principle later aided computer system scientist Jennifer Golbeck uncover a Russian bot network on Twitter. She noticed that for most buyers, the variety of followers that their followers have adheres to Benford’s law, but artificial accounts considerably veer from the pattern. She utilised identical strategies to catch persons who acquire bogus retweets. Examples of Benford’s regulation utilized to fraud detection abound, from Greece manipulating macroeconomic information in its software to join the eurozone to vote-rigging in Iran’s 2009 presidential election. The message is very clear: organic processes generate figures that favor small leading digits, whilst naive approaches of falsifying facts do not. 

Why does nature make a dearth of nines and a glut of ones? First, it’s important to state that several facts sets do not conform to Benford’s legislation. Grownup heights generally start off with 4s, 5s and 6s when calculated in toes. A roulette wheel is just as very likely to land on a range beginning with 2 as with 1. The law is additional probable to spring from data sets spanning several orders of magnitude that evolve from particular types of random processes. 

Exponential growth is a especially intuitive illustration. Picture an island that is at first inhabited by 100 animals, whose populace doubles just about every yr: right after 1 year, there are 200 animals, and right after two a long time there are 400. Now we discover one thing curious about the leading digits. For the full duration of the initially 12 months, the initially digit of the population dimension of the island was a 1. On the other hand, in the 2nd yr inhabitants counts spanned the 200s and 300s for the same period of time, leaving considerably less time for every single top digit to reign. This carries on, with 400 to 800 in the third yr, where the top digits retire quicker however. The notion is that to grow from 1,000 to 2,000 necessitates doubling, while escalating from 8,000 to 9,000 is only a 12.5 p.c raise, and this trend resets with every fresh order of magnitude. There is very little distinctive about the parameters we chose in the island case in point. We could start off with a populace of 43 animals and develop by a issue of 1.3 per 12 months, for illustration, and it would produce the identical correct pattern of major digits. Practically all exponential expansion of this sort will tend towards Benford. 

The law’s stubborn indifference toward units of evaluate presents a different hint as to why the sample is so typical in the natural environment. River lengths observe Benford’s legislation whether or not we history them in meters or miles, whereas non-Benford-complying details like grownup heights would radically alter their distribution of main digits when converted to meters, as no person is 4 meters tall. (Remarkably, Benford’s is the only main digit distribution that is immune to these kinds of unit adjustments.) We can imagine of modifying models as multiplying each worth in our data established by a selected quantity. For illustration, we would multiply a set of lengths by 1,609.34 to change them from miles to meters. Benford’s legislation is really resilient to a substantially additional typical transformation. Getting Benford-complying data and multiplying each and every entry by a various selection (alternatively than a preset one like 1,609.34) independent of the knowledge, will leave the main digit distribution unperturbed. This implies that if a normal phenomenon occurs from the item of quite a few unbiased resources, then only 1 of those resources will have to accord with Benford’s regulation in order for the overall consequence to. Benford’s regulation is cannibalistic, a great deal in the exact same way that if you multiply a bunch of figures with each other, only one of them requires to be zero for the total result to be zero. 

These explanations account for several appearances of the pattern, but they never clarify why the assorted collection of figures plucked from an problem of Scientific American would show Benford’s regulation: these figures really do not grow exponentially, and we’re not multiplying them with each other. Mathematician Ted Hill found what several contemplate to be the definitive evidence of the foremost digit legislation. His argument is regretably rather technological, but in simplistic terms states that if you decide a bunch of random figures from a bunch of random facts sets (in math conditions, chance distributions), then they will have a tendency towards Benford’s legislation. In other words and phrases, although we have observed that plenty of details sets clearly show Benford’s sample, the most reputable way to achieve it is to pull figures from various resources, like people we see in a newspaper. 

I have used a great deal of time thinking about Benford’s regulation, and irrespective of the tapestry of explanations, it continue to surprises me how frequently it takes place. Spend awareness to the quantities you encounter in your everyday everyday living and you could start to place it.

This is an viewpoint and analysis short article, and the sights expressed by the author or authors are not essentially those people of Scientific American.